BQ #7: Unit V: Derivatives and the Area Problem

The difference quotient is a something we have come across earlier in Math Analysis. However, the question now is, how are we able to derive this? Where does this come from? Presently, with our newfound knowledge of calculus, we know that the difference quotient basically is the first step towards finding our derivative (the slope of all tangent lines). On a side note, we know that in order to find the derivative, we do the difference quotient, then find the limit of it, as h approaches 0. But again, we go back the question of how did we get the difference quotient in the first place? Look at the picture below for better clarification--I will explain below.

http://cis.stvincent.edu/carlsond/ma109/DifferenceQuotient_images/IMG0470.JPG

I mentioned before that the derivative is basically the SLOPE of all tangent lines. When you hear slope, you should think of the formula we use to find the slope: (y-y)/(x-x) (rise over run). We are going to use this formula and basically, plug a few more things in to make it the difference quotient. In order for us to the the slope formula, we need to know two points. Look at the graph above. That first point, we will assume that the x value is just "x". Thus, the y value must be "f(x)". So, our first point is (x, f(x)). Our second point ,we move further across the x axis. We will call the distance crossed "h". So the x value would be x+h. So, it only makes sense that our y value is f(x+h). Our second point is (x+h, f(x+h)). Now that we have our two points, we will plug it in our slope formula. So your plugged in slope formula should be [f(x+h)-f(x)]/[x+h-x]. We simplify the bottom because the x's cancel out and you are left with this: [f(x+h)-f(x)]/h. THE DIFFERENCE QUOTIENT. 

Now you know where the difference quotient comes from. However, in calculus, we proceed further, as I mentioned before. If you were trying to find the slope, the derivative, you would find the limit as h approaches 0. Your main question is probably why is h approaching zero. The thing is, we want to be able to find our tangent line (a line that touches the graph at one point). The problem is that we a secant line, where we touch the graph TWICE (as you can see the red line is touching the blue line twice in the picture above). So, in order for us to get one point, we can basically have those two points on top of each other... meaning that they are in the same place. We are able to get them to sit on top of each other by decreasing the "h", the distance between the two points. The smaller "h" is the closer the two points are. Therefore, we have our limit as h approaches 0 because we can't actually have it at 0, but we can get it pretty darn close. 

This is just a hint of what calculus has in store, and I'm still waiting for the rest to be revealed! This is my final blogpost and I hope these posts have helped in some way or another because I know I've learned a lot this year. I've conquered Math Analysis and no lie... I feel like a Mathematician. I'm done! Lights out. *Nox* 

References: 

http://cis.stvincent.edu/carlsond/ma109/DifferenceQuotient_images/IMG0470.JPG

BQ #6 - Unit U

1. What is continuity? What is discontinuity?
With functions in real life, we deal with both continuity and discontinuity. Continuous graphs entail of many characteristics: predictability (meaning you are able to know where the graph is going), the lack of breaks, holes, and jumps (because it is CONTINUOUS), and the ability to be drawn without lifting your pencil. Knowing this, we can also note that in a continuous graph, all limits should be equivalent to its values (if this is not completely understood, it will be clearer with further information). Basically, continuity is seen in many of the graphs dealt with in earlier years of math (in regular parabolas, linear graphs, etc).
Discontinuity is the opposite, as you can already guess. Discontinuous graphs have breaks, jumps, and holes, meaning you WILL need to lift your pencil from the paper in order to draw these graphs. There are four specific discontinuities found in these types of graphs. The four discontinuities branch into two categories: removable and non-removable. The only discontinuity that is removable is a point discontinuity. These occur when we have a hole in the graph.

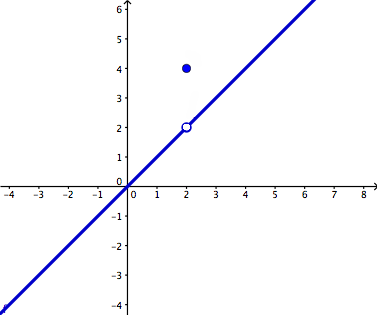Point Discontinuity (http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif)

There are three non-removable discontinuities: jump discontinuity, oscillating behavior, and infinite discontinuity. Jump discontinuities occur when our left and right limits do not match. Look at the picture below to understand this better.

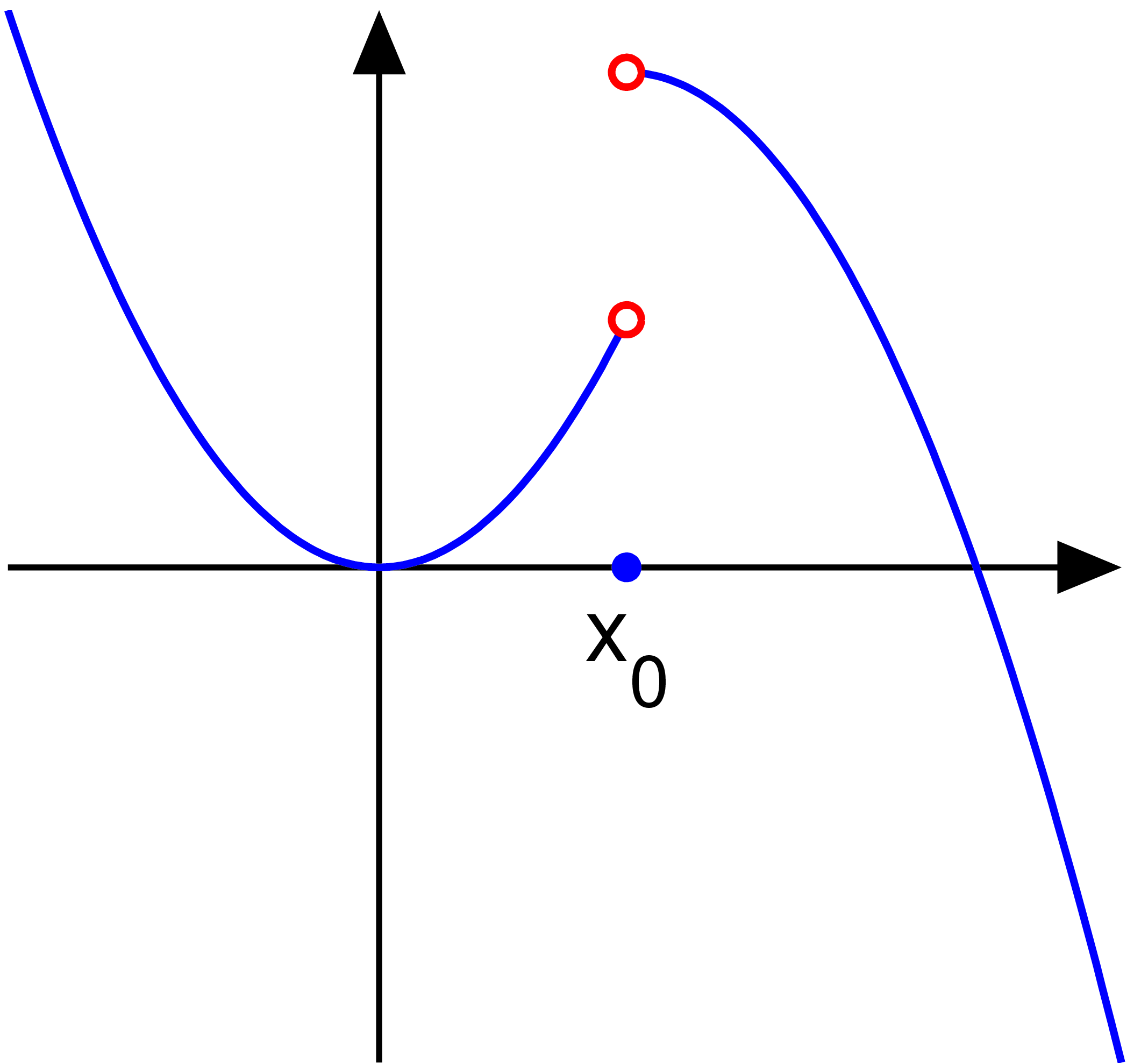Jump Discontinuity (http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.png)

Oscillating behavior occurs wherever you see "wiggles". 

Oscillating behavior (http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg)

Infinite discontinuity occurs when a vertical asymptote is present which leads to unbounded behavior. 

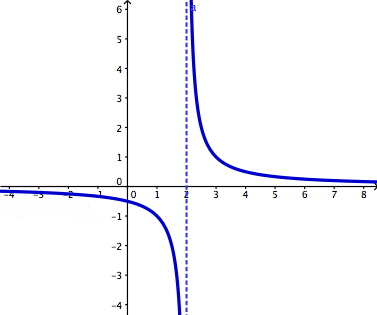Infinite Discontinuity (http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif)

2. What is a limit? When does a limit exist/not exist? What is the difference between a limit and a value? 

A limit is the intended height of the graph. Think of it as where the left and right are intended to meet. You and your friend are meeting at a diner but come from different ways. As long as the two sides meet, your limit exists. Let's go further into this. We now know what a limit is but where does the limit exist and where does it not. 

I mentioned briefly in the section above about limits. In continuous graphs, the limit always exists because the graph continuously intends to reach the same point. Let's go into our discontinuities again. Looking back at the point discontinuity, understand that our limit does exist here despite the hole present. Remember, a limit is the INTENDED height, meaning we intended to get there. A hole marks the place that we intended to get to. Think of it like you and your friend tried to meet at the diner but the diner moved somewhere else. You two still should have ended up at the same place. 

Now, sometimes...

I'm sorry, I had to. (http://media.tumblr.com/tumblr_m1eqlrQcTf1qdt09k.gif)

The limit does not exist at those three non-removable discontinuities we discussed earlier. The question though is why? The limit does not exist at a jump discontinuity because we have different left, right limits, as I said before. When I say this, I mean that the left and right sides of the function just don't match up; they do not meet the same INTENDED height. It is as if you and your friend went to two different diners, you didn't meet up with each other. With jump discontinuities, because the limit does not exist, we have side limits, our left and right limits that I mentioned before. These side limits look practically the same as our limit notation (the limit as x approaches a # of f(x) is equal to L) (http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit01.jpg). The only difference is that our side limits have a (+) and (-) next to that c, our number. A c- is from the left limit; a c+ is from the right limit. 

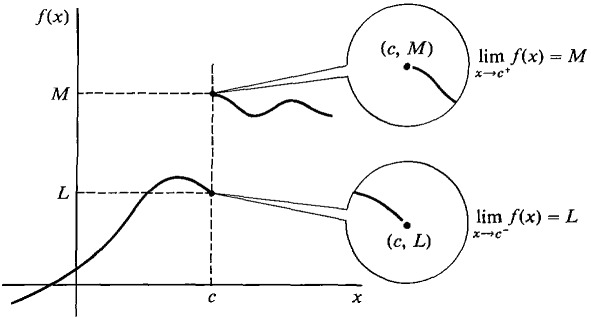One Sided Limits (right limit, top; left limit, bottom) (http://www.vias.org/calculus/img/03_continuous_functions-69.gif)

Moving on, the limit does not exist when dealing with oscillating behavior. It is practically impossible to actually see the limit of this graph (because of so many wiggles). Truthfully, it does not approach a single value. 

Finally, the limit does not exist when we have an infinite discontinuity. As stated before, this discontinuity exists when we have a vertical asymptote which leads to unbounded behavior. This basically means that it is approaching infinity but really, we can never approach infinity because it is not an actual numerical value. That is why our limit does not exist. 

Just to clarify as well, we understood earlier that a limit is the INTENDED height of a function. Therefore, it is good to know that the value is the ACTUAL height of a function. 

(http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif)

I used this picture below but it provides a good example of a limit and a value that are different. The hole in the graph is our limit. Why? Take your fingers and place one to the left and one to the right of the graph. Inch them closer and closer to one another. Notice how they INTEND to reach the hole. They intend to reach that hole, therefore, that is our limit. However, above that hole, we have an actual point, our VALUE because it is the ACTUAL height of the function. 

I mentioned this before though, our limit and value are not always different. In continuous graphs, our point where we intend to reach (the limit) is also the actual value of the graph. 

3. How do we evaluate limits numerically, graphically, and algebraically? 

We use tables to evaluate limits numerically. We take a limit and find x values that approach it and find out. You want to find 3 values to the left of the value and 3 to the right. From there, you would trace these x values (in your graphing calculator) and find the y value. By finding the y values you should notice whether or not they are approaching each other towards a common limit or not. For better understanding, watch the video below, as they go over it more in depth. 

Graphically, we take our left and right finger and basically trace ourselves. We first plug our function into the y=screen of our graphing calculator. Then, we go to GRAPH and we TRACE. We trace to the value we are looking for basically.
Sometimes, we are actually given a graph. If this occurs, you place your figners to the left and right of where you want to evaluate a limit. Wherever your fingers meet, you have a limit. If they do not meet, your limit does not exist. The video below shows better visual for this process.

Finally, we can evaluate limits algebraically. There are three ways to do this; direct substitution, dividing/ factoring out, and rationalizing/ conjugate.
Direct substituion is where we basically take the x value that we are approaching and plug it into the function. There are four possibilities. You could end up with a numerical answer, 0/# (still 0), #/0 (undefined, which means the limit does not exist), and 0/0 which is indeterminate form. If you ever get indeterminate form, you use another method.
The dividing out/ factoring method is used when we get indeterminate form. What we do here is factor what we can. If you get x^2-9 you factor that into (x-3)(x+3), and other things of that sort (sum and difference of cubes will pop up as well). If factored correctly, you should be able to cancel something out. After canceling out terms, you should be left with a simpler function. Plug in the number that you are approaching and you should get your answer.
Rationalizing/ conjugate method is used if you cannot factor out--most likely, you have a radical. All you need to do is multiply the entire fraction by the conjugate. You take the conjugate of the term that has the radical. (If you do not know what the conjugate is, it is basically changing it from say this: 3x+1 to this: 3x-1. You just change the sign). You should be able to cancel terms out after FOILing. Plug the number into the simplified problem and you get your answer.
In the video below, they go over examples of the three ways to algebraically solve limits. (The video is a little shaky, but the content is there).


References:
1.http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif
2. http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.png
3. http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg
4. http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif
5. http://media.tumblr.com/tumblr_m1eqlrQcTf1qdt09k.gif
6. http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit01.jpg
7. http://www.vias.org/calculus/img/03_continuous_functions-69.gif
8. https://www.youtube.com/watch?v=8z4aofW85K4
9. https://www.youtube.com/watch?v=aVcqrDFcaCA
10. https://www.youtube.com/watch?v=CvB4080WC48

BQ#4 – Unit T Concept 3

Why is a “normal” tangent graph uphill, but a “normal” Cotangent graph downhill? Use unit circle ratios to explain.
Asymptotes play such a large part in the reason why "normal" tangent graphs go up and why "normal" cotangent graphs go down.
Tangent, as discussed before, has the ratio of y/x or sine/cosine. With this knowledge, we know that whenever our x-value/cosine is 0, we will have an asymptote. Well, if we think about it, at pi/2 (0,1) and 3pi/2 (0,-1), our x-value is 0. These are where are asymptotes lie. Now, thinking back to our unit circle, we know that from pi/2 to pi, we go into Quadrant II, where only sine is positive--in other words, tangent is negative. So, in our first half of the space between our two asymptotes, our values are negative. Moving on, we know that pi to 3pi/2 in the unit circle is Quadrant III where tangent is positive. So, our other half of the space between our two asymptotes is going to be positive. Looking at the entire picture, we would see that our tangent graph begins at the bottom and goes up, making it uphill!
Cotangent has the same idea. Its ratio is x/y or cosine/sine. We want sine/our y-value to be 0 in order to find our asymptotes. So, the only places in the unit circle where we have 0 as our y-value are at 0 radians (1,0) and pi (-1,0). Therefore, our asymptotes are at 0 and pi. Again--same idea. From 0 to pi/2, we have Quadrant I where all trig functions are positive; cotangent is positive. However, from pi/2 to pi, we have only sine being positive so cotangent is negative. Guess what? That is what we are going to be seeing on our cotangent graph. Our first half of the space between the asymptotes is basically Quadrant I, so our graph will have positive values. However, our second half of the period is in Quadrant II where we established the fact that cotangent is negative. Our graph will go down. So, looking at the entire graph as a whole, we see that our graph starts from top to bottom, going downhill.

BQ#3 – Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.
Sine and cosine are found in the ratio identities of the rest of the four trig functions; they affect each one of those trig functions because of this.
Tangent
With tangent, we know that tangent is equal to sine over cosine. Now, just by knowing the values of sine and cosine, we can assume what tangent will be on the graph. Look at the visual below to better your understanding.

(https://www.desmos.com/calculator/cwdr1eyszr)

        If you look at the red highlighted area, that is 0 to pi/2, so basically the first quadrant. Even without looking at this graph, we know that sine and cosine are positive, so tangent must be positive as well (positive divided by a positive is a positive). And you can see this translate on the graph. If you look at the green cosine values and the red sine values, you can tell they are above the x-axis, meaning they are positive. And, we determined that since those to trig functions are positive, tangent must be positive, which it is (the orange line). You can see the same thing going on in the next parts of the graph. In the "Quadrant II", on the graph, you can tell that cosine is negative (as the green values fall below the x-axis) and sine is positive (as the red values are above the x-axis). And because of our ratio identity of tan(x)=sin(x)/cos(x), we know that a positive divided by a negative makes a negative. That is why the tangent values fall below the x-axis this time. The 3rd quadrant, again, look at our sine and cosine values: they are both negative. So, a negative divided by a negative is a positive: tangent values are positive. Finally, you should be understanding the relationship that tangent, cosine, and sine have. The last part of the period, cosine is positive (values are above the x-axis) and sine is negative (values below the x-axis); tangent is negative. 

         Now, that you know why the tangent graph looks as it does (through the understanding of its relationship with sine and cosine), we need to deal with another part of these graphs: the asymptotes. The asymptotes are not just there because we say so. There is a reason behind it. Remember when we talked about how tan(x)=sin(x)/cos(x)? We are using this identity again. We know that asymptotes are created when we have an undefined value. We get undefined values when we divide by 0. So, knowing that... we look to our ratio identity and see that cosine must equal 0 in order to get an undefined value (because we are dividing by cosine). How do we get cosine to equal 0? Well, we know that cosine is essentially the x-values of certain points in our unit circle. The only parts of the unit circle that have 0 as an x-value are pi/2 (0,1)and 3pi/2 (0, -1). Therefore, these marks on the graph are where we have asymptotes! Look at the graph above and see where it seems like the tangent graph discontinues; do you notice that pi/2 and 3pi/2 are where we don't really see the tangent graph go? That is because of the asymptotes! 

Cotangent

Cotangent has sine and cosine in its ratio identity as well. Cot(x)=cos(x)/sin(x). 

(https://www.desmos.com/calculator/cwdr1eyszr)

Cotangent has the same thing going on as we saw in tangent. Remember to look at the values of the sine and cosine graphs and relate them to cotangent. For example, see how sine and cosine values are positive, so we have cotangent as positive. However, in the green section, we see that sine (the red graph) has positive values and cosine (green graph) has negative values; we can deduce that cotangent is negative because a negative divided by a positive is a negative. 

Because cotangent has a different ratio than tangent, we are going to be having some different ratios. The ratio identity of cotangent is cot(x)=cos(x)/sin(x). Again, asymptotes are undefined values, meaning they are divided by 0. So, because sine is our denominator in this ratio, sine must be equal to 0 in order to find asymptotes. Where on our unit circle do we have sine=0? Sine is y/r, basically the y values of the unit circle. So, we know the only parts of the unit circle where the y values are 0 are 0 (1,0) and pi (-1,0). Knowing this, we know that our asymptotes are at 0 radians and pi. Look at the graph above and check to make sure. Notice how at 0 radians, a new period begins, as if we lifted our pencil to create a new part of the graph. The same is seen at the pi mark. 

Secant

Secant is a little different from tangent and cotangent. Its ratio identity is 1/cos(x).

(created at https://www.desmos.com/calculator)

We have the same idea though, as we saw in the previous graphs. If cosine is negative, then secant values must be negative as well. If cosine is positive, the secant graph must be positive as well. You can see this in the graph. The cosine values (the black graph) are positive in the red shaded part of the graph; and look at that, the secant graph (the red graph) is positive in that section as well. You can see the trend in the following sections/quadrants as well. It is good to remember that the sine values in here do not have any effect on the secant graph because it is not part of its ratio (*disregard the orange sine graph in the picture above*). 

The asymptotes of secant are the same as we saw in tangent. Tangent had cosine as the denominator as well. So, we know that at pi/2 (0,1) and 3pi/2 (0,-1) there are going to be asymptotes for this secant graph. 

Cosecant

Cosecant has the same idea as secant just reversed, like we saw with cotangent and tangent. Cosecant's ratio identity is csc(x)=1/sin(x). 

(created at https://www.desmos.com/calculator)

Again, we remember that if sine is positive on the graph, then cosecant must be positive as well, because 1 divided by a positive is always a positive--and vice versa. You can see in the red shaded part, the sine graph (the orange line) is positive and the cosecant graph (the red line) is positive as well. It is good to remember that cosine has no effect on cosecant because it is not found in the ratio (*therefore, disregard the cosine graph in the picture above*). 

Cosecant has its asymptotes wherever sine is 0 (because we are dividing by sine in this ratio). Looking back to our cotangent graph, we remember that sine was 0 at 0 radians and pi (because of the coordinates of (1,0) and (-1,0)). So, we will have cosecant's asymptotes at 0 radians and pi. That is why, if you look at the picture above, you see that the graph seems to cut out at 0 radians and pi. 

BQ#5 – Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

Sine and cosine do not have asymptotes because their ratios are y/r and x/r, meaning that the radius will ALWAYS be the denominator. You will never have a 0 as your denominator. Because of this, we will never encounter an undefined answer, meaning we will not encounter any asymptotes (since asymptotes = undefined, basically).

However, that is a different case for cosecant, secant, cotangent, and tangent. Cosecant has a ratio of r/y. The "y" value can be 0 in certain cases: if we are at (1,0) or (-1,0). Same for secant; secant has a ratio of r/x and x can be 0 in some cases: (0,1) and (0, -1). Cotangent and tangent have the ratios of x/y and y/x so, again, of course you will have some y values and x values that equal to 0.

Also, a good thing to nice is that cotangent and and cosecant have the same denominator in their ratios: y. Therefore, they will have the same asymptotes. Tangent and secant will have the same asymptotes as well because their denominators in their ratios are x.

BQ#2 – Unit T Concept Intro

How do the trig graphs relate to the unit circle?
Trig graphs, believe it or not, are essentially the unit circle unwrapped (at least in one period). BAM. Let's think about what we already know about the unit circle. We are going to use sine as an example, first. In the case of sine, the 1st and 2nd quadrants are positive whereas the 3rd and 4th quadrants are negative. Now, the 1st quadrant goes from 0 radians to pi/2. The 2nd quadrant goes from pi/2 and pi. So from this information alone, we can deduce that from 0 to pi, our values are going to be POSITIVE. The 3rd quadrant goes from pi to 3pi/2; the 4th goes from 3pi/2 to 2pi. Because sine is negative in these quadrants on the unit circle, in the trig graphs, from pi to 2pi, our values are going to be negative. Thus, the whole entire graph will go up and then down, because it is corresponding with the values we know from the unit circle.

 

As you see, the same can be seen for other trig functions. For cosine, we have the pattern being positive, negative, negative, postive. Therefore, on the graph, you will see the period beginning with positive values, but dipping at pi/2 and becoming negative. At pi, it remains negative, but when you hit the mark of 3pi/2, our values will be positive, as it should.

 

Tangent and cotangent are similar however there is a special situation with them (which I will go into further detail in the next section). Anyway, our graph for tangent/cotangent will begin with positive values, then negative values, then positive, and negative. However, if you notice, we have a pattern already seen in the first two quadrants, that is then repeated in the next two quadrants--which leads us into the next question!

 

Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?
The period for sine and cosine is 2pi because the pattern finishes at 2pi and does not repeat until we begin another "revolution" around the unit circle. The pattern is +,+,-,- for sine. The pattern is +, -, -, +. You see, you need all quadrants in order to explain the FULL pattern. You need to go around the unit circle in ONE FULL revolution. So, your period will go to 2pi.

The period for tangent and cotangent is only pi. Why? Look at the picture above. Do you notice that the pattern is +, -, +, -? The pattern repeats itself twice in one revolution of the unit circle. Why do we want to repeat that? So, we only really need the first quadrant in order to fully explain the pattern. That is why tangent and cotangent periods only go to pi.

 

Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

So why is it that we have amplitudes of one for sine and cosine? Think about it. Sine has the ratio of y/r. Cosine has the ratio of x/r. R can only equal 1, since the radius of a unit circle has to be 1. So, the values x and y can only go up to 1 themselves. So if you can only divide 1 by 1 to get the largest number... your largest value can only be 1/ -1. That is why sine and cosine cannot equal something greater than 1 or less than -1. However, think about the other trig functions and their ratios. Tangent is y/x. You are not restricted to values between -1 and 1 because you are dividing by different numbers that vary from being just 1 and -1. Same is for cotangent but backwards. Also, for trig functions like cosecant and secant, you have r/y and r/x. You can divide your "r" (1) by a small number like 1/2 and end up with 2. That is why those other funcitons do not have amplitudes.

Reflection #1: Unit Q: Verifying Trig Identities

1. When a problem asks you to "verify a trig identity", it basically means to work out one side of the equation, simplifying it to the point to where it equals the other side. It is almost as if the problem gave you the starting and ending points and you are just finding the steps to get from one to the other.

2. First of all, make sure you memorize all the identities. They're honestly not that difficult to remember after dealing with them SO MUCH, and it is a nice thing to know that this equals this at the top of your head. However, sometimes just knowing these identities, does not do anyone any good. I find changing everything in terms of cosine and sine makes everything a lot easier. What I like to say is "When in doubt, do sine and cosine." and it's pretty much true. Also, u substitution was such a blessing on my mind. It basically allows us to replace a trig function with "u" when we have a quadratic on our hand. Trust me, you do not want to be "x-boxing" or factoring or FOILing (sinx +1)^2. I don't know if these can actually be called "tricks" that helped me get through this unit, but I know these reminders saved my life on the test. For verifying, it is essential for you to know that touching the "right side" (the side that you're usually trying to work towards), is a BIG NO NO. Another thing I found helpful was knowing that whenever you square anything, you are going to end up with extraneous solutions; as a result, you will need to make sure you actually plug your answers into the original equation to ensure the "correctness" (is that a word...?) of the answer.

3. Whenever I see a problem that asks to verify, I get excited because they practically told you what you're supposed to end up with! Now you just have to find your way to the end. My general thought process is, "Are there any trig functions that can convert to sine and cosine?". If I see cotangent or cosecant, and so on (you get the point), I would usually replace them with sine and cosine. However, sometimes that does not work for me, so my next thought is "Are there any trig functions that are squared?" Usually, if something is squared, I would replace that with a Pythgagorean Identity, and then go from there. If I see that I have a binomial as my denominator, I will multiply the entire fraction by the conjugate. If I see two/ multiple fractions being added together, I will make sure the two have the same denominator, and if they don't (which is 90% sadly), then I would have the lowest common denominator (LCD) between the two, multiply each fraction with what is needed to achieve that LCD, and then combine them so I have one large fraction.  Again, I really only focus on the left because we don't really need to do anything to the right. This is just really what I think in general, and my thinking will change depending on the types of problems I am given. Ultimately, the best piece of advice I could give to you when dealing with verifying is just to go through it slowly and rationally. Don't feel the need to rush and you'll be able to get through these like nothing.

SP#7: Unit Q Concept 2: Finding All Trig Functions When Given One Trig Function and Quadrant

This SP7 was made in collaboration with Sarahi Leal. Please visit the other fantabulous, supercalifragilisticexpialidocious posts on her blog by going here.

Solving with Identities:

Solving with SOH CAH TOA: 

The idea we want you to formulate is that there are two ways to find these trig functions: using identities and using SOH CAH TOA. When dealing with identities, it is always best to remember to know WHERE the unknown triangle falls in. As you can see in our very first step, we determined what quadrant the triangle is in, just by knowing what quadrants certain trig functions are positive and such. Another good thing to remember, especially as we deal with identities more and more, is that when you square root a trig function (as seen in #4 of "Solving with Identities"), you will end up with two possible answers because it is both negative and positive. However, we were able to conclude that it was positive because sine and cosecant are positive within Quadrant II. Always remember these little nuances because they do help in making these types of problems easier. 

I/D3: Unit Q - Pythagorean Identities

Inquiry Activity Summary: 
1. sin2x+cos2x=1 
This is a Pythagorean Identity (a proven fact/formula that is always true), so, we will be using the Pythagorean Theorem in order to begin deriving it. Originally, our Pythagorean Theorem is a^2 + b^2 = c^2. However, we learned in recent units that we deal with triangles on graphs, specifically when we are dealing with the Unit Circle. The same situation is still present, therefore we want to adjust our formula. The legs of your triangle are measured in how much you go left/right on the graph (x-axis) and how much you go up/down (y-axis). We also remember that our hypotenuse of our triangle is also the radius of the Unit Circle. So we go from a^2 + b^2 = c^2, to x^2 + y^2 = r^2. Now that we have our "new" Pythagorean Theorem, we continue on and think of how on earth we simplify it into our Pythagorean Identity.
Our formula is  x^2 + y^2 = r^2. We want to get to sin2x+cos2x=1. To do that, we divide everything by r^2. If we divide everything by r^2, we get this: x^2/r^2 + y^2/r^2 = 1 (r^2/r^2). Already, we can tell that r^2 divided by r^2 is 1. Now we can look at the other parts; x^2/r^2 is basically (x/r)^2 and y^2/r^2 is (y/r)^2. Immediately, you should notice something about these variables and RATIOS. The ratio for cosine is x/r. The ratio for sine is y/r. *AHA MOMENT*
Now that we are aware of this relationship, let's plug them into our formula. So, (x/r)^2 becomes cos^2x and (y/r)^2 becomes sin^2x. Finally, we end up with cos^2x + sin^2x = 1.

This picture is clarification of what I described in the text ABOVE. 

Don't believe that it actually works? We can use any of the "Magic 3" ordered pairs from the Unit Circle to show that it is true. Look in the picture BELOW to see how I used the 60 degrees ordered pair in order to prove this identity true.

Simple matter of plugging in numbers into our identity and verifying. 

2. Other Pythagorean Identities 

Now that we have our main Pythagorean Identity, we will use it to find our other two. 

• The first Pythagorean Identity contains secant and tangent. The only way to get that is by dividing by either cosine or sine. For this one, we want to divide everything by cosine because the ratios will simplify into what we want: tangent and secant. We divide sin2x by cos2x and we get tan2x. How do I know? Besides from memorizing this identity, we can use logic. Sine's ratio is y/r and it is being divided by cosine's ratio, which is x/r. Another way we can look at that is y/r TIMES r/x. So as a result we have y/x which is tangent. Cosine divided by cosine is simply 1. And 1 divided by cos2x is sec2x (because secx = 1/cosx; we just powered up because everything is being multiplied in this reciprocal identity). The picture below gives clarification of what you should be left with.

This is what our Pythagorean Identity is. 

• The other Pythagorean Identity contains cosecant and cotangent. Because we divided the last identity by cosine, we want to divide by sine this time. We divide sin2x by sin2x and get 1. We divide cos2x by sin2x and we get cot2x. (x/r TIMES r/y = x/y). We divide 1 by sin2x and we end up with csc2x. The picture below will have the Pythagorean Identity and work along with it. 

This is what our 3rd Pythagorean Identity looks like. 

Inquiry Activity Reflection: 
1. “The connections that I see between Units N, O, P, and Q so far are…” the continual use of trig functions (and the things we are able to use with them), and the references towards Unit Circles and the triangles within it.
2. “If I had to describe trigonometry in THREE words, they would be…” Ratios. Are. Everywhere.

WPP #13 and 14: Unit P Concept 6 and 7: Law of Sines and Law of Cosines

This WPP #13 and 14 was made in collaboration with Tina N. and Sarahi L. Please visit the awesome, fantabulous blog post here! And make sure to check out Tina N.'s awesome blog posts here!

BQ #1: Unit P Concept 3 and 4: Law of Cosines and Area of an Oblique Triangle

Law of Cosines
1. Why do we need it?

• When dealing with real life examples of things like triangles, we need to realize that not all of these situations are ideal. There will be triangles that are not right triangles but we still need to know what to do with them. This is where the Laws of Cosines comes in handy. With this, we will be able to find missing parts of practically any triangle, may it be a right triangle or a non-right triangle.
• We can only use Law of Cosines when we are given SSS (all three sides) or SAS (side, angle, side).

2. How is it derived from what we already know? 

http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm

• At first glance, it is obvious that this triangle is not a right triangle. As a result, we drop a perpendicular from angle B to create two right triangles (ABD and BCD). We want to identify the perpendicular as "h" (the height) and the distance between angle A to the right angle (D) as "r". 
• From here, we can begin our derivation. For this, we want to find the distance between angle B and C (side a, basically). If we were to plot this triangle on the graph (beginning at the origin), angle C would be plotted at (b,0) because we move b units on the x-axis and we do not move at all on the y-axis. Angle B would have the ordered pair of (cCosA, cSinA). We are able to get these values with our knowledge of trig functions. Looking at cosA, we know that it is equal to r/c (adjacent/hypotenuse). Now, "r" is the amount of units we go on the x-axis, therefore, we want to change cosA = r/c to r = cCosA. That is why our x-value for Angle B is cCosA. The reason why we have cSinA as our y-value is because sinA = h/c (opposite/hypotenuse), and after we manipulate the equation, we discover that h = cSinA. "H" is the amount of units we go up, therefore, cSinA is our y-value. 
• Now that we have these two points, we can plug them into our distance formula. We use the distance formula because we are trying to find the distance/length between angle B and C. 

• In order to have an easier problem we can work with, we square both sides of the equation to get rid of the square root. Now, we can begin substituting certain values for others in order to shape the distance formula into our Law of Cosines. 

http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm
*Keep in mind that these values were plugged in d^2 = (y-y)^2 + (x-x)^2 (just a different arrangement)*

• Because we are looking for the distance between angles B and C, also known as side a, we change the "d" to an "a", allowing us to be more specific. Now we plug in the values. First, we plug in the y-values: cSinA and 0. Because subtracting 0 does nothing, we leave cSinA by itself in the parentheses. In the next set of parentheses, we plug in the x-values: b and cCosA. That is how we get (b - cCosA). 
• We want to expand these values next, so we foil them as we would with polynomials. From expanding (cSinA)^2, we get c^2sin^2A. When we expand (b - cCosA)^2, we get -2bcCosA + c^2cos^2A. 
• It looks overwhelming now, but we can simplify the equation by taking out c^2 and leaving the rest of the problem. At this point, we are left with (sin^2A + cos^2A) within the parentheses. Because of this, we are able to simplify it to 1. 
• The reason why we can simplify sin^2A + cos^2A is because it is like our Pythagorean Theorem. x^2 + y^2 = r^2. If we divide everything by r^2, we get (x^2/r^2) + (x^2/r^2) = 1 (r^2/r^2). We know from our knowledge of trig functions that cosine is x/r and sine is y/r. Therefore, when we square cosine and sine we get (x^2/r^2) and (x^2/r^2). That is why we are able to have (sin^2A + cos^2A) equal 1. 
• Now, because we are only multiplying c^2 by 1, we are left with the final equation: a^2 = c^2 + b^2 - 2bc cosA. Keep in mind that we are able to derive this equation for different sides of the triangle using similar processes. If we were looking for side b or c, we would end up with similar equations. 

http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm
*These are the Law of Cosines variations for different sides of the triangle other than side a*

Area of an Oblique Triangle:

1. How is the “area of an oblique” triangle derived?

http://hotmath.com/hotmath_help/topics/law-of-sines/law-of-sines-image015.gif

• We usually rely on our perpendicular bases and heights in order to find areas of triangles. However, oblique triangles do not have perpendicular bases and heights, so we must create them ourselves, either by dropping a perpendicular, or drawing one ourselves.
• Our regular formula is A = 1/2(bh). What we really need to know is our height since 1/2 is a given and "b" is usually already known. We are going to be using our trig functions once more. We will use angle B as an example. Sin B = h/c (h being the perpendicular drawn). Remember that we are looking for "h". As a result, we multiply both sides by c to discover that h = cSinB. Now that we know "h", we can substitute it in the area formula. Now we have A = 1/2(bcSinB). This is our formula for the area of an oblique triangle!



http://wps.prenhall.com/esm_blitzer_algtrig_2/13/3560/911520.cw/index.html

• There are different variations of the formula since we can use different angles (depending on what we are given in the problem).
• We must be given two sides and an angle in between them (SAS) in order to use this.

2. How does it relate to the area formula that you are familiar with?

• We use the original formula (A = 1/2(bh)) as a starting point to find the area formula for an oblique triangle. We still use the same base, however we have to find our own "h" by using trig functions (sine).

Works Cited: 

1. http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm

2. http://hotmath.com/hotmath_help/topics/law-of-sines/law-of-sines-image015.gif

3. http://wps.prenhall.com/esm_blitzer_algtrig_2/13/3560/911520.cw/index.html

WPP #12: Unit O Concept 10: Angles of Elevation and Depression

(http://cdn.c.photoshelter.com/img-get/I0000NJw_WS3ZrAc/s/900/900/cribbar-newquay-20111030-11.jpg)

Kim Nana decided to go surfing since she closed the coffee shop for the day. She gets on her surfboard and begins riding a wave when she notices a larger wave in front of her. She measures the angle of elevation to the wave in front of her to be 38* and the angle of depression (the very bottom of the wave) to 42*8'. If she is 80 feet away from this wave, how tall is the taller wave in front of her? Round to the nearest foot. 

Please remember to try to do the problem on your own before looking at the pictures. 

I/D2: Unit O - Derive the SRTs

Inquiry Activity Series:

1. 30-60-90 triangle
In order to derive this triangle, we first need to begin with an equilateral triangle and go from there. The equilateral triangle's characteristic is that it has the same side measures for each of the three sides. In this case, our equilateral triangle will have side measures of 1. Another thing we should take note of is that an equilateral triangle is also an equiangular triangle which means all of the angles are of the same measure as well. So, because a triangle's angles must always add up to a sum of 180, we can concur that each of the three angles will be 60 degrees (180/3=60).
Now that we remember the basic knowledge of our equilateral angle, we can begin to shape it into a 30-60-90 triangle. The first thing we want to do is split the triangle in half. By doing this, we create a 90 degree angle inside. We also, by dividing the triangle in half, we divide an angle in half. By splitting this angle we create a 30 degree angle on one side of the equilateral triangle. Thus, we technically create two 30-60-90 degree triangles--but we only want to look at one.

Above, we can see the transformation from an equilateral triangle to a 30-60-90 triangle. We have the angles, so now we want to find the actual sides--the important part. As you can see in the photo, 1/2 is written across the 30 degrees. I was able to get the value 1/2 with simple logic. Each side length was 1 and because we split the triangle in half, I also split that bottom side in half. So we know that the side across the 30 degrees is 1/2 and the side across the right angle is 1. Now the question is, what is the side across the 60 degrees, the side we created by splitting the triangle in half. We are going to determine this side with the help of our friend Pythagoras, and his Pythagorean Theorem. 

Pythagorean theorem: let legs be "a" and "b" and hypotenuse be "c"

In the above picture, I used the basic knowledge of the Pythagorean Theorem to find our 2nd leg. After working it out (look at the picture), I discovered that our unknown side has the length of √3/2. Finally, we know all sides of the 30-60-90 triangle!

I placed the letters that the values corresponded with in the Pythagorean Theorem.

We are not completely done quite yet. Dealing with the fractions can be quite annoying at times (correction: all the time) so we want to multiply each side by 2 in order to create nice numbers. Side "a" would be 1, side "b" would be √3, and side "c" would be 2. If you notice, even if we did not multiply by 2, side "c" is twice the amount of "a" and side "b" is basically side "a" multiplied by √3. This is where we begin to derive the 30-60-90 triangle. The relationships I pointed out are found in multiples of these sides. If we add those "n" into the picture, we see this relationship. Our side "a" (across the 30 degrees) would be "n" because it is only 1. Side "b" (across 60 degrees) would be n√3 because it is side "a" multiplied by √3 (as we discussed). Side "c" (across the 90 degrees) would be 2n because our hypotenuse is twice the length of side "a". The reason why we place "n" is to emphasize the fact that this relationship is always there with these angles even with different numbers from the ones we found in the above picture. It is like ratios where they do not all have the same numbers but have the same relationship (ex: 1:2 is the same as 2:4). 

The final 30-60-90 triangle derived from the equilateral triangle. 

2. 45-45-90 Triangle

We want to derive this triangle from a square. Refreshing our knowledge of squares, we know that all sides are equal, all angles add up to 360, and each angle is equal to each other. Using quick mental math we know that each angle will have to be 90 degrees (360/4=90). Our square we will be using has side lengths of 1. From here, we want to create a 45-45-90 triangle and the only way to do that is draw a diagonal through the square. Like we saw in the 30-60-90 triangle, we are going to see our angles split. Two angle will be split in half (because of the diagonal) so those angles will be 45 degrees. We now have a 45-45-90 triangle. 

Now, we have both sides across the 45 degrees: they are equal to 1. But now, we want to know what the measure of the hypotenuse (the dotted line) is in order to find the relationship between these numbers. Let us return to the Pythagorean Theorem!

Knowing the two legs allows us to find our hypotenuse, which is radical 2.

We now know each of our sides. Both legs are equal to 1 while the hypotenuse, we just found, is equal to √2. Comparing the sides with one another, we see that the legs are 1 while the hypotenuse is radical 2 multiplied by the legs (1). These are the values when we use a square with the sides of 1. However, the idea we want to understand is that this relationship extends beyond one specific triangle with specific lengths. This is where we substitute "n" into the triangle. We want "n" to take the place of 1 (because we have ONE "n"). So our legs (a&b) are going to be "n". Our hypotenuse (across the 90 degrees), because it is 1 times radical 2 (radical 2 times the length of side "a" or "b"), will be n times radical 2. "N" allows the possibility of different lengths and measures of these sides but still contains the relationship found in the 45-45-90 triangle. 

We found the relationship between the sides of a 45-45-90 triangle!

Inquiry Activity Reflection:

1. “Something I never noticed before about special right triangles is…” is that they are derived from these sort of shapes (the equilateral triangle and square) in order to justify why we have these numbers (they are not just randomly given).
2. “Being able to derive these patterns myself aids in my learning because…” if I forget the values of the sides, I can easily use my knowledge of pythagorean theorem to find them.

I/D #1: Unit N Concept 7: How do SRTs and the UC relate?

Inquiry Activity Summary: 
The activity we did in class had us recalling our knowledge of special right triangles from geometry. We discovered that these same right triangles are seen within our unit circle. Thus, by setting our radius to 1 (because a unit circle ALWAYS has a radius of 1), we can determine the lengths of each side of the triangle. As a result, we can then find the actual ordered pairs of the points of the triangles that create the angles of 30, 45, and 60 degrees.

(http://upload.wikimedia.org/wikipedia/commons/1/15/Triangle_30-60-90_rotated.png)

1. This is a 30 special right triangle. The side across from the 30 degrees (the shortest side) is equal to x. The side across from the 60 degrees (adjacent to the 30 degrees) is equal to  x√3. The side across from the 90 degree angle is equal to 2x. 

(https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiFw_yhWi1CV1w3RqOUrjPmoZ4KTj8Enp8JqJlpqLkJvTeYwXGRKzfpj0MRUIvUT9pBNS55uVLVffyPa7jigCyFXy9PoHL1nH7i_7B9MP4ROYjwGhXuZc4jKDB0XhyIThUL59BJtzcNFAk/s1600/special+right+triangle.jpg)

2. This is a 45 special right triangle. The side across from the 45 degrees is equal to x. Because we have two equal angles (another 45 degree), the side opposite of the other 45 degree (or adjacent to the 45 degree angle to the very left) is also x. The hypotenuse has the length of x√2. 

(https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiFw_yhWi1CV1w3RqOUrjPmoZ4KTj8Enp8JqJlpqLkJvTeYwXGRKzfpj0MRUIvUT9pBNS55uVLVffyPa7jigCyFXy9PoHL1nH7i_7B9MP4ROYjwGhXuZc4jKDB0XhyIThUL59BJtzcNFAk/s1600/special+right+triangle.jpg)

3. This is a 60 special right triangle. This triangle is basically like the 30 special right triangle,  but the 30 and 60 degrees have switched places. The side across the 60 degree is x√3. The side across the 30 degree is x. The side across the 90 degree is 2x. 

4. The use of these triangles enables us to understand why ordered pairs resemble things like (1/2, rad3/2). We now understand the meaning of these numbers: they are the values of the sides created by the angles. In order to find the values of all the sides of these triangles WITHIN a UC, we take all the values of the sides and divide by the hypotenuse. We divide the hypotenuse by itself in order to have it equal to 1. Because we divided the hypotenuse by itself, we must do the same to each of the other sides, and divide by the hypotenuse as well. 

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/
image022.gif)

This triangle is on a coordinate plane, a graph. Take into consideration of what is your x-axis and your y-axis and remember that your triangle begins at the CENTER (0,0). 

By now we know the values of each of the sides for a typical 30 degree special right triangle. Now, we want to find the length within a UC. As stated before, we need to divide each side by the hypotenuse. The hypotenuse is equal to 2x so 2x/2x=1. Our radius/hypotenuse is 1, which we want. Move on to the 30 degree side: that equals x, so x/2x (cancel out the x's) equals 1/2. Our vertical side (our "y" side) is equal to 1/2. Move on to the 60 degree side: x √3, so x√3/2x (x's cancel out) equals √3/2. Our horizontal side (our "x" side) is equal to √3/2. Now, looking at the blue point in the picture above, we now know that on the x-axis (because this is in a graph), the distance is √3/2. We also know that the distance, looking at the y-axis, to the point is 1/2. This is how we get the ordered pair (√3/2, 1/2).

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/
image036.gif)

Again, remember this is on a graph. Your angle begins at (0,0). Your horizontal distance is essentially your x value. Your vertical distance is your y value.

Divide each side by the hypotenuse once more. Your hypotenuse in a 45 degree angle equals x√2. The hypotenuse divided by itself is 1. Each side across the 45 degree (they are the same length) is x. Divide x by x√2. The x's cancel leaving 1/√2. Rationalize by multiplying the top and bottom by √2. Thus, each leg of the triangle in a UC is equal to √2/2. Now, with this knowledge, we can find the ordered pair of the point, shown above. The horizontal side/x value is equal to √2/2. The vertical side/y value is equal to √2/2. Taking these two to find our ordered pair, we are given the coordinate of (√2/2,√2/2). 

(http://00.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_13.gif)

This is the same exact idea we have discussed in the two previous pictures (basically the 30 degree angle values but switched). We divide all sides by the hypotenuse (2x) and we get the values of 1/2 for the horizontal/x value side and √3/2 for the vertical/y value side. Again, we know this is on a graph, with the triangle beginning at the origin. We use these values to find the coordinate of the 60 degree triangle which is (1/2, √3/2). 

The values of the ordered pairs are explained through these special right triangles, basically the distance of one leg and another. It is also worth noting that for the quadrant angles (0, 90, 180, 270, & 360 degrees) have much simpler ordered pairs. The 0 degree does not create any angle and lies on the positive x-axis. Because we know that the radius is 1, we know that the ordered pair for the 0 degree is (1,0) because 1 is radius (on the x axis) and it lies on the x-axis (explaining the 0). Similar situations are found for the other quadrant angles: 90 degree has the ordered pair of (0,1), 180 degree has the ordered pair of (-1,0), 270 has the ordered pair of (0,-1), and 360 shares the same ordered pair as 0 degrees (they share the same coterminal side). 

5. These triangles lie within the first quadrant. However, we can redraw these triangles in the other quadrants but still find the same patterns seen in the first quadrant. 

(http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_34.gif)

This picture displays the 30 degree triangle just in different quadrants. As you can see, they share the same values as we saw in the first quadrant. HOWEVER, looking closely, you should notice the negatives on certain values. In quadrant 2, your x value turns negative, as it should, considering that is the negative x-axis. In quadrant 3, both valeus are negative since you have the negative x-axis and the negative y-axis. Finally, quadrant 4 shows the ordered pair to have a negative y value because you have the negative y-axis. 

(http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_45.gif)

This picture has a 45 degree triangle in quadrant 2. Again, we see the same values that we talked of in quadrant 1. However, in this quadrant, our x-value is negative because of our negative x-axis. 

(http://02.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_21.gif)

This picture displays the 60 degree triangle in quadrants 3 and 4. In quadrant 3, the values are the same as in the first quadrant, but both values are negative because it falls in the negative x and y axes. In quadrant 4, the values are the same as well, except only the y-value is negative because it falls in the negative y-axis. 

Inquiry Activity Reflection:

1. “The coolest thing I learned from this activity was…” how we were able to find the values of the ordered pairs through special right triangles.

2. “This activity will help me in this unit because…” it reasoned why we had the numbers that we had. I struggled with understanding why we had such numbers. I used to memorize but never completely understood the meaning of these numbers. Now, if I forget one, I can recall special right triangles and find it easily.

3. “Something I never realized before about special right triangles and the unit circle is…” that just by knowing the basics of these special right triangles, allows you to achieve a better understanding of the unit circle.

Work Cited:
1.http://upload.wikimedia.org/wikipedia/commons/1/15/Triangle_30-60-90_rotated.png
2. https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiFw_yhWi1CV1w3RqOUrjPmoZ4KTj8Enp8JqJlpqLkJvTeYwXGRKzfpj0MRUIvUT9pBNS55uVLVffyPa7jigCyFXy9PoHL1nH7i_7B9MP4ROYjwGhXuZc4jKDB0XhyIThUL59BJtzcNFAk/s1600/special+right+triangle.jpg
3. http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_
RESOURCE/U19_L1_T3_text_final_3_files/image022.gif
4. http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE
/U19_L1_T3_text_final_3_files/image036.gif
5. http://00.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_13.gif
6. http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_34.gif
7. http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_45.gif
8. http://02.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_21.gif